Luigi Guido Grandi acreditava ter encontrado a prova matemática da Criação ao estudar uma série matemática infinita, semelhante à série geométrica de Euclides.
A Matemática é uma ferramenta poderosa que pode ser usada para explicar fenômenos complexos, desde o funcionamento do universo até a estrutura da matéria. Embora seja difícil determinar se a Matemática pode explicar o significado da vida, é inegável que ela desempenha um papel fundamental em nossa compreensão do mundo ao nosso redor.
Uma das áreas da Matemática que pode nos ajudar a entender melhor o universo é o Cálculo, que estuda as taxas de mudança e a acumulação de quantidades. Além disso, a Geometria e a Álgebra também são fundamentais para a compreensão de fenômenos complexos, como a estrutura do espaço e a relação entre variáveis. A busca por respostas é um desafio constante e a Matemática é uma ferramenta essencial nessa jornada. Com símbolos como ∑ e ∞, a Matemática pode parecer intimidadora, mas é exatamente essa complexidade que a torna tão fascinante.
Matemática: O Enigma da Série Grandi
A Matemática é uma disciplina que nos desafia a resolver problemas complexos e entender conceitos abstratos. Uma dessas questões é a série Grandi, que consiste em uma soma infinita de 1 e -1 alternados. Essa sequência parece simples, mas ao ser repetida ao infinito, torna-se um desafio para os matemáticos desde o século 18.
A pergunta é: qual é o resultado dessa soma infinita? Uma resposta intuitiva é que não há resposta, pois a soma oscila entre 0 e 1 sem chegar a um valor único. No entanto, essa é apenas uma das quatro opções consideradas ao longo do tempo. A mais surpreendente é a que mais convenceu o primeiro matemático a chamar a atenção para esse quebra-cabeça.
O Matemático Luigi Guido Grandi
O padre, filósofo, matemático e engenheiro Luigi Guido Grandi (1671-1742) foi o instigador dessa questão. Nascido em Cremona, na Itália, Grandi demorou a desenvolver seu interesse pela Matemática, mas com seu primeiro livro, ‘Geometrica divinatio Vivianeorum problematum’, publicado em 1699, ele ganhou reconhecimento em seu país e no exterior.
Sua reputação o levou a se tornar o matemático da corte do Grão-Duque da Toscana, Cosme 3º de Medici, em 1707. Nesse cargo, ele foi responsável por importantes projetos de engenharia, incluindo a drenagem do Vale de Chianna. Além disso, ele colaborou na publicação da primeira edição das obras de Galileu Galilei (1718) e publicou uma versão italiana dos ‘Elementos’ de Euclides (1731).
Grandi também aconselhou o Papa Clemente sobre a reforma do calendário e introduziu na Itália as ideias de Gottfried Leibniz sobre Cálculo. Ele foi admirado no exterior e se tornou membro da prestigiada Royal Society of London em 1709, depois de Isaac Newton publicar seu trabalho sobre teoria musical.
A Série Grandi e a Rosa Polar
Uma das obras mais admiradas de Grandi foi o estudo da rosa polar, uma família de curvas que lembram flores, que ele chamou de rhodoneas (do grego rhodon, rosa), em seu livro ‘Flores Geometrici’ (1725). No entanto, foi outra obra sua que despertou não só o interesse de seus pares, mas também uma acalorada polêmica em torno da série que leva seu nome.
No livro ‘Quadratura do Círculo e da Hipérbole’, publicado em 1703, Grandi estudou a soma infinita de 1 e -1 alternados. Ele observou que, adicionando parênteses, chegava-se a resultados diferentes. (1 – 1) + (1 – 1) + (1 – 1)… resultava em 0 + 0 + 0…, que é igual a 0. Mas se fosse escrito assim: 1 + (- 1 + 1) + (- 1 + 1) + (- 1 + 1)… então a soma seria 1 + 0 + 0 + 0…, o que daria 1.
Isso por si só já era surpreendente. Mais surpreendente ainda foi ele afirmar que a soma de infinitos 0s é igual a 1/2. Grandi preferiu explicar esse resultado com uma parábola em que imaginava dois irmãos que herdaram dos pais uma joia valiosa. Eles foram proibidos de vendê-la e dividi-la à metade destruiria seu valor. Os irmãos concordaram que alternariam a propriedade da joia, criando uma situação semelhante à série Grandi.
Essa questão continua a ser um desafio para os matemáticos e é um exemplo de como a Matemática pode ser complexa e fascinante. A Álgebra e a Geometria são fundamentais para entender essa questão, e o Cálculo é essencial para resolver problemas como esse. A série Grandi é um exemplo de como a Matemática pode ser usada para resolver problemas complexos e entender conceitos abstratos.
Fonte: © G1 – Globo Mundo
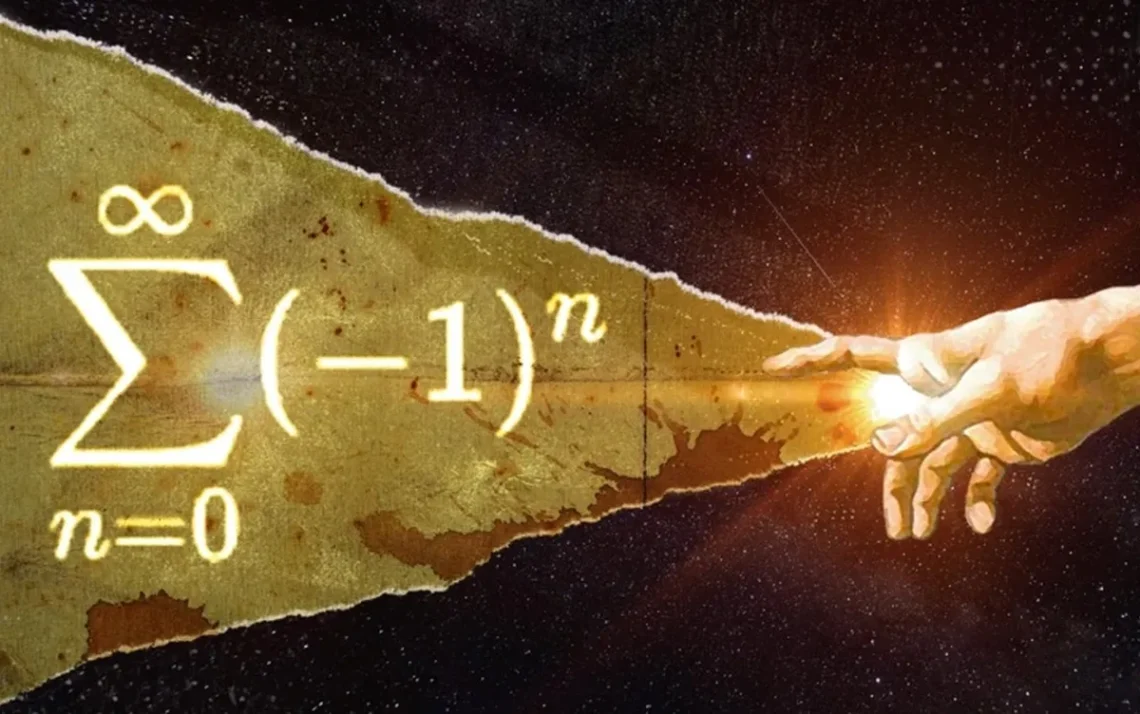







Comentários sobre este artigo